
Rectilinear (a.k.a. uniform) grids are among the simplest type of grid. The grid axes are parallel to the coordinate axes and the cells are always rectangular in cross-section. The positions of all the nodes can be computed knowing only the coordinate extents of the grid (minimum and maximum x, y and optionally z). Two-dimensional rectilinear grids are comprised of quadrilateral cells. For a 2D grid with i nodes in the x direction and j nodes in the y direction, there will be a total of (i - 1)*(j - 1) cells.
The connectivity of the cells (the nodes that define each cell) can be implicitly determined because the nodes and cells are numbered in an orderly fashion. The advantages of rectilinear grids include the ease of creating them and the uniformity of cell area in 2D and cell volume in 3D. The disadvantages are that grid nodes are generally not coincident with the sample data locations and large areas of the grid may fall outside of the bounds of the data. A simple two-dimensional rectilinear grid is shown in Figure 1.9.

Figure 0.8 Two-Dimensional Rectilinear Grid
Three-dimensional rectilinear grids offer the simplest method for gridding a volume. They are constrained to rectangular parallel piped volumes and have hexahedral cells of constant size. (See Figure 1.10) For some processes and visualization techniques such as volume rendering, this is advantageous and may even be required. For a grid having i by j by k nodes there will be (i-1) * (j-1) * (k-1) hexahedron cells whose connectivity can be implicitly derived.

Figure 0.9 Three-Dimensional Rectilinear Grid
The following type of grid derives its name from the numerical methods that it employs. Simulation software such as the USGS's MODFLOW utilizes a finite difference numerical method to solve equilibrium and transient ground water flow problems. This solution method requires a grid that contains only rectangular cells. However the cells need not be uniform in size. For two-dimensional grids, this results in rectangular cells, however it is possible that no two cells are precisely the same size. Some simulation software requires that finite difference grids be aligned with the coordinate axes. EVS does not impose this restriction, but it does provide a means to export the grid transformed so that the grid axes are aligned. Figure 1.11 shows a rotated 2D finite difference grid. Smaller cells are concentrated in areas of the model where there are significant gradients in the data. For groundwater simulations this is usually where wells are located. For environmental contamination it should be the location of spills or areas where DNAPL (dense non-aqueous phase liquids) contaminant plumes were detected. The smaller cells provide greater accuracy in estimating the parameter(s) of interest.
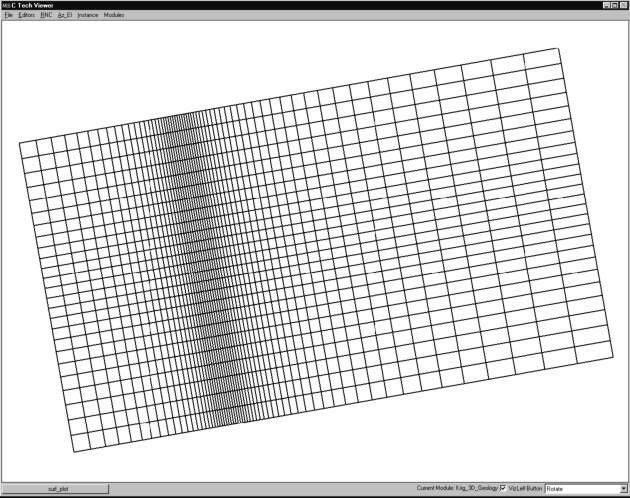
Figure 0.10 Two-Dimensional Rotated Finite Difference Grid
Three-dimensional finite difference grids have the same restrictions as 2D grids with respect to their x and y coordinates (cell width and length). However, the z coordinates of the grid (which define the cell thicknesses) are allowed to vary arbitrarily. This allows for creation of a grid that follows the contours of geologic surfaces. For a grid having i by j by k nodes there will be (i-1) * (j-1) * (k-1) hexahedron cells whose connectivity can be implicitly derived. However the coordinates of the nodes for this grid must be explicitly specified. Figure 1.12 shows the grid created to model the migration of a contaminant plume in a tidal basin.
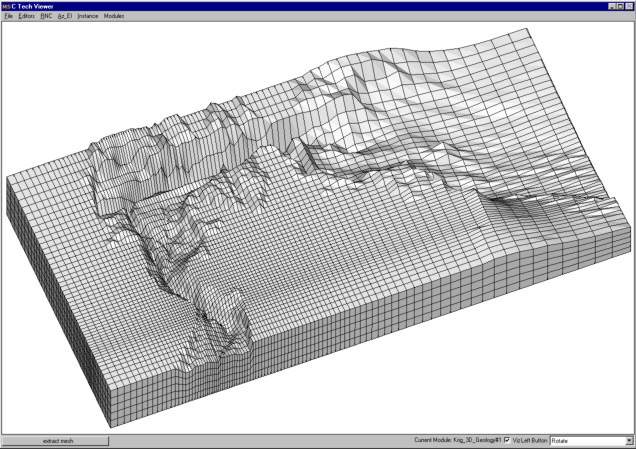
Figure 0.11 Three-Dimensional Finite Difference Grid
© 1994-2018 ctech.com